箱线图（又称箱须图）作为数据可视化的核心工具，能够高效呈现数据分布特征与异常值，是科研分析、商业决策和质量管理中的必备技能。本文将系统解析箱线图的组成原理、使用方法及统计趋势解读技巧，结合2025年最新实践指南，帮助读者掌握从数据可视化到深度分析的完整流程。

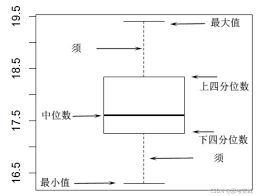
核心概念：箱线图的定义与构成

箱线图（Box Plot/Box-and-Whisker Plot）是基于五数摘要（最小值、第一四分位数Q1、中位数Q2、第三四分位数Q3、最大值）的统计图表，由美国统计学家John Tukey于1977年提出。其核心价值在于用简洁的图形语言展示数据的集中趋势、离散程度和异常值，尤其适合多组数据对比分析。

关键组成要素解析

• 箱体（Box）：从Q1（25%分位数）延伸至Q3（75%分位数），包含数据中50%的核心样本，箱体长度代表四分位距（IQR=Q3-Q1），反映数据的离散程度。
• 中位数线：箱体内的水平线，标记Q2（50%分位数），直观展示数据的集中位置，其偏离箱体中心的程度可初步判断分布偏态。
• 胡须线：从箱体两端延伸的垂直线，默认覆盖Q1-1.5×IQR至Q3+1.5×IQR的范围，标识数据的正常波动区间。若数据极值未超出此范围，胡须线直接延伸至最值。
• 离群值：超出胡须线范围的独立数据点（用圆点/星号标注），代表潜在的异常值或极端值，需结合业务场景判断其意义（如数据错误或真实极端事件）。

应用场景与价值：箱线图的实战意义

箱线图凭借其简洁高效的特性，已成为跨领域数据探索的基础工具，典型应用场景包括：

跨组数据对比分析

在医学研究中，箱线图可直观对比不同治疗组的疗效指标（如血压变化、肿瘤缩小体积），通过箱体位置、长度及离群值分布，快速识别组间差异。例如，AJE（美国期刊编辑协会）2025年发布的临床研究指南中，明确推荐使用箱线图展示实验组与对照组的连续变量分布，以替代传统的均值±标准差表述，更全面反映数据全貌。

数据分布特征诊断

教育领域常用箱线图分析学生成绩分布：若中位数线接近箱体中心且胡须线对称，提示成绩呈正态分布；若中位数靠近Q1且上胡须线较长，表明数据右偏（存在少数高分学生拉高整体水平）。某重点中学2024年高考成绩分析显示，数学科目箱线图呈现明显右偏，促使教学团队针对性加强基础薄弱学生辅导。

质量控制与异常监测

工业生产中，箱线图可实时监测关键指标波动（如零件尺寸、产品合格率）。阿里云Quick BI商业分析平台2025年新增的箱线图预警功能，通过动态计算IQR范围，当生产数据出现离群值时自动触发警报，帮助某汽车零部件厂商将质检异常响应时间缩短40%。

技术原理：从五数摘要到胡须线计算

核心参数计算步骤

以某电商平台12个月销售额数据（单位：万元）为例：[120, 135, 140, 150, 130, 125, 160, 170, 180, 190, 200, 210]

• 排序数据：[120, 125, 130, 135, 140, 150, 160, 170, 180, 190, 200, 210]
• 计算四分位数：
• Q1（第25%位置）：(130+135)/2=132.5  
• Q2（中位数）：(150+160)/2=155  
• Q3（第75%位置）：(180+190)/2=185  
• 确定胡须线范围：
• IQR=185-132.5=52.5  
• 下限=132.5-1.5×52.5=53.75（实际取最小值120，因无数据低于此值）  
• 上限=185+1.5×52.5=263.75（实际取最大值210）  
• 离群值判断：本例所有数据均在[120,210]范围内，无离群值。

变体与扩展形式

• 改良箱线图：允许自定义胡须线倍数（如金融风控场景常用3×IQR减少误判），或对长尾分布数据采用对数刻度转换。
• 小提琴图：融合箱线图与核密度曲线，既保留五数摘要信息，又展示数据分布形态细节，适合需要深度分析数据形状的场景（如用户行为研究）。

2025年专家实践指南：进阶技巧与趋势解读

多维度分析策略

现代数据分析工具（如Power BI、Tableau）支持通过颜色编码、分面排列实现箱线图的多变量对比。例如，某快消品牌通过“地区（行）×季度（列）×产品类别（颜色）”的箱线图矩阵，同时分析不同维度的销售额分布差异，发现华南地区Q4护肤品销售额中位数显著高于其他区域，进而调整区域营销策略。

动态交互与参数优化

2025年主流BI工具新增实时IQR调整功能：默认1.5×IQR适用于一般场景，而制造业质量控制可提高至2×IQR以减少误报，科研数据探索可降低至1×IQR以捕捉更多潜在异常。某医疗设备公司通过动态调整参数，成功从MRI设备运行数据中识别出早期故障征兆，将设备故障率降低28%。

联合可视化方法

Editverse 2025年数据可视化指南强调：箱线图擅长异常值识别，但难以展示分布模态（如是否为双峰分布），建议与直方图联合使用。例如，某大学录取分数箱线图显示存在离群值，结合直方图发现实际是特长生单独计分形成的第二峰值，避免误判为数据异常。

实操案例：Python绘制与解读箱线图

以下代码使用matplotlib绘制上述销售额数据的箱线图，并解读统计趋势：

import matplotlib.pyplot as plt

# 示例数据：某产品月销售额（单位：万元）
sales_data = [120, 135, 140, 150, 130, 125, 160, 170, 180, 190, 200, 210]

# 绘制箱线图
plt.figure(figsize=(8, 6))
box = plt.boxplot(sales_data, vert=True, patch_artist=True,
                 boxprops=dict(facecolor="lightblue", color="black"),
                 whiskerprops=dict(color="black"),
                 medianprops=dict(color="red", linewidth=2))

# 图表美化与标注
plt.title("2024年度产品销售额箱线图分析", fontsize=14)
plt.ylabel("销售额（万元）", fontsize=12)
plt.grid(axis="y", linestyle="--", alpha=0.7)
plt.text(1.1, 155, f"中位数: {box['medians'][0].get_ydata()[0]}万", fontsize=10, color="red")
plt.text(1.1, 132.5, f"Q1: {132.5}万", fontsize=10)
plt.text(1.1, 185, f"Q3: {185}万", fontsize=10)

plt.show()

输出解读：
- 箱体从132.5万延伸至185万，表明中间6个月销售额集中于此区间，业务稳定期占比50%。
- 红色中位数线（155万）接近箱体下沿，提示数据轻微右偏，即存在较多高销售额月份（如190万、200万、210万）拉高整体水平。
- 胡须线覆盖全部数据范围，无离群值，说明年度销售未出现极端异常波动，业绩表现平稳。

局限性与风险规避

尽管功能强大，箱线图仍有以下局限需注意：

小样本数据偏差

当样本量<20时，四分位数计算误差增大，离群值判定可能失真。例如，10个数据点的箱线图中，Q1和Q3易受个别值影响，建议此时改用茎叶图或直接展示原始数据。

分布形态信息缺失

箱线图无法展示数据的模态特征（如是否为双峰分布）或尾部厚度，强偏态数据（如收入分布）需结合QQ图验证是否符合特定理论分布（如对数正态分布）。

工具计算差异

不同软件的四分位数算法存在细微差异：Excel采用线性插值法，R语言默认使用“类型7”算法，Python matplotlib则采用Numpy的percentile函数。跨工具分析时需统一计算标准，避免结论冲突。